Modellando l'evoluzione di CoVID-19 in Italia

6 marzo 2020

In base ai dati aggiornati al 5 marzo, 77 paesi hanno segnalato la presenza del nuovo coronavirus (CoVID-19) nei loro territori, portando il numero globale di persone infette a 93,090. L'Italia è ora il terzo paese per numero di persone infette, con 2.502 casi confermati, e seconda solo alla Cina per numero di decessi (80).

Dall'inizio dell’epidemia sono stati pubblicati molti modelli di diffusione di CoVID-19, ma a causa della sua origine la maggior parte dei lavori si e’ concentrata sull’evoluzione in Cina. In questo articolo vogliamo presentare un modello dell'epidemia di CoVID-19 in Italia, nonché predire i possibili scenari in base alle risposte della politica.

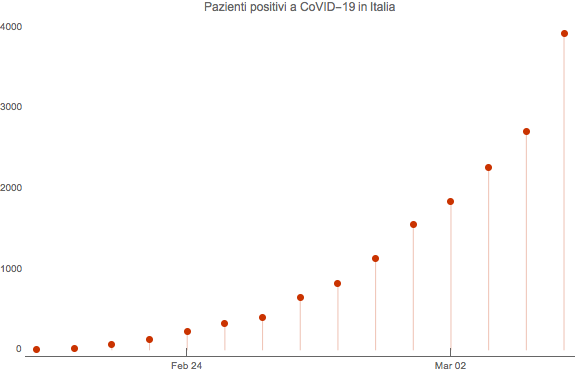
Come è possibile modellare un fenomeno così complesso, che dipende da fattori quali la biologia, le interazioni sociali, gli interessi economici e la politica (solo per nominarne alcuni)?

Bisogna formulare alcune ipotesi.

Per studiare la diffusione delle epidemie è stata sviluppata una classe di modelli, chiamati SIR, che storicamente ha dimostrato di essere in grado di approssimarne l’evoluzione futura.

L'idea è innanzitutto di considerare un'isola, dove non sono consentite né l’entrata né l’uscita di persone. Ogni persona può trovarsi in uno dei seguenti stati in un dato momento: "Suscettibile", "Infetto" e "Recuperato" (da qui l'acronimo S-I-R). Con una certa probabilità le persone che non hanno mai avuto la malattia (S) possono ammalarsi e infettarsi (I) per un certo periodo prima di guarire (R). Si presume che gli individui guariti (R) non possano più essere infettati (quindi anche i decessi rientrano in questa categoria). Nel caso di CoVID-19, è opportuno estendere il modello con uno stato aggiuntivo, "Esposto", comprendente le persone che hanno il virus ma non sono ancora infettive (modello SEIR).

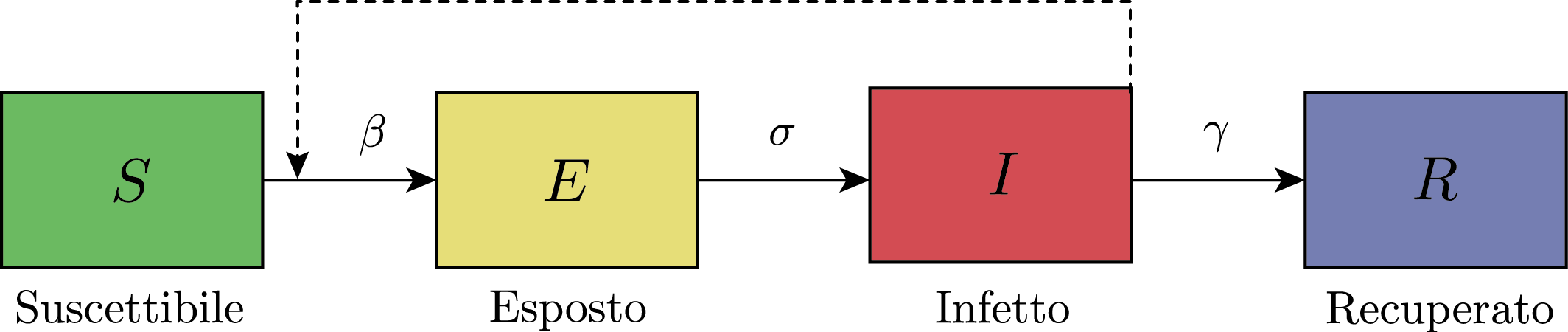
I parametri del modello dipendono da due fattori:

1. Dettagli sulla dinamica del virus (non troppo difficile da stimare);

2. Dettagli sulla mobilità e l'interazione tra esseri umani (molto più complessi da dedurre).

Con questo insieme di ipotesi siamo in grado di condensare la ricchezza delle interazioni tra il virus e gli esseri umani in un unico numero, chiamato R0. Questa quantità rappresenta un concetto piuttosto semplice: "Dato che sono malato, quante persone infetterò? (In media)". Supponiamo ad esempio, che la persona A sia malata e che il nostro sistema preveda un R0=2. Ciò significherebbe che A infetterà 2 persone. Quelle 2 persone infetteranno a loro volta 4 persone, le quali infetteranno altre 2 persone ciascuna (quindi 4 * 2 = 8) e così via. Questo mette in luce il fatto che la diffusione della malattia è di tipo moltiplicativo, piuttosto che additivo.

Ma come possiamo adattare tutto ciò alla situazione italiana? La carenza di dati rende difficile predire precisamente R0, ma osservando l’evoluzione storica è possibile stimare questa quantità misurando la rapidità di crescita degli infetti.

Ma, ehi, perché nell’immagine sono presenti due R0? Perché la società può ridurre le interazioni tra le singole persone come meccanismo di protezione per ridurre la diffusione della malattia. Ad esempio, grazie alla chiusura di scuole e palestre, lo svolgersi degli eventi sportivi senza pubblico, il rinvio di concerti e in generale la riduzione delle interazioni sociali, si abbassa la possibilità di contagio tra individui. Tutto ciò si traduce nella riduzione di R0 e il suo effetto può essere visto nell’immagine: la linea arancione mostra la progressione della malattia con il suo ritmo "naturale", mentre la curva blu mostra come l'aggressività della crescita sia almeno parzialmente mitigata da queste norme (bisogna tener conto che le politiche di contenimento impiegano un certo tempo per avere impatto sui dati).

È abbastanza? Stiamo soddisfatti con un R0 = 1.7?

Da questo modello emerge un risultato importante: la malattia si diffonde a tutta la comunità se R0>1, mentre la malattia è destinata a scomparire rapidamente se R0<1.

Quindi perché dovremmo interessarci ad abbassare ancora R0 se comunque rimane sopra 1?

Anche se la teoria prevede che dopo molto tempo la maggior parte degli abitanti nell'isola verrà infettata dal virus (con R0> 1), è fondamentale valutare la rapidità con cui avverrà questo processo. In particolare, la riduzione di R0 aiuta ad abbassare il numero di persone malate contemporaneamente. Teniamo presente che il nostro sistema sanitario ha risorse limitate (ovvero un numero fisso di letti di unità di terapia intensiva) e potrebbe non essere in grado di garantire cure adeguate a fronte di una domanda eccessiva.

Ma ora basta con la teoria. Cosa ci racconta la simulazione?

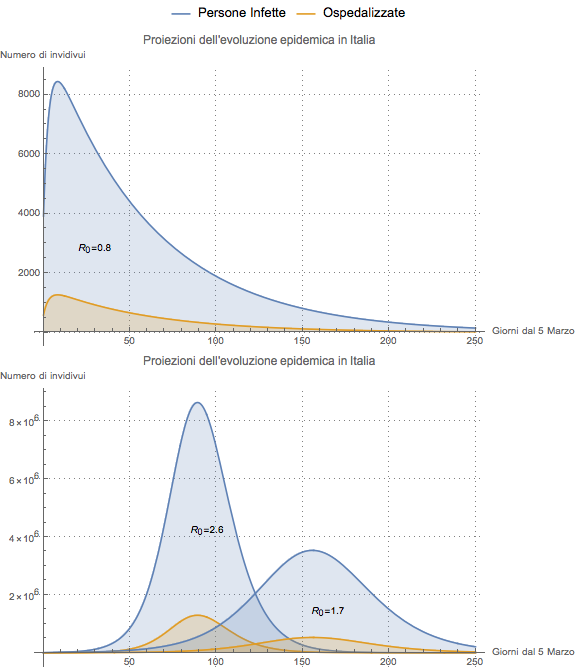
Prima di tutto: questo scenario rappresenta la proiezione di “Cosa succederebbe se..?”. In particolare il grafico risponde alla domanda "Cosa accadrebbe se lasciassimo evolvere la situazione così com’è (senza misure di contenimento)?" Queste immagini dovrebbero aiutarci a riflettere su alcune cose:

1. Con R0 <1, l’evoluzione tende in modo naturale e relativamente rapido alla scomparsa della malattia;

2. È sempre utile abbassare R0, poiché mantiene il picco più basso e lo sposta più in là nel futuro (minor impatto sul sistema sanitario);

3. Dovremmo agire, e dovremmo farlo rapidamente. Non dovremmo lasciarci ingannare nel pensare che ogni giorno abbiamo "x persone in più di ieri". Dovremmo iniziare a vedere il quadro più ampio rendendoci conto che abbiamo "x volte più persone di ieri".

Se osserviamo con attenzione la stima di quante persone avranno bisogno di un ricovero in ospedale (corrispondente a circa il 9% degli infetti, come riportato da salute.gov.it) e lo confrontiamo con la capacità del Sistema Sanitario Nazionale, la preoccupazione diventa molto più evidente.

È ragionevole aspettarsi che i governi imporranno vincoli più severi (*) sulla mobilità delle persone nel tentativo di ridurre la R0. Le misure pratiche che dovranno essere prese sono il risultato del compromesso tra i danni economici causati dalle politiche di contenimento (come la mancanza di produttività) e i danni economico-sociali che accadranno nel caso in cui non verrà effettuato alcun contenimento (sistema sanitario sovraccaricato, persone deboli e anziane in grave pericolo). È tuttavia importante considerare non solo le ripercussioni economiche, ma il bilancio in termini di sofferenza e vite umane.

Quindi, in conclusione, citando John Oliver: "Quanto dovremmo preoccuparci?"

La risposta è: "Probabilmente un po'."

È evidente come il panico non serva a nulla, ma una consapevole attenzione al problema può aiutarci a comprenderlo meglio e ad agire in modo efficace. Bisogna trovare la via di mezzo tra il correre nudi per strada gridando all'Apocalisse e il bollare questo evento come una “banale influenza”, vivendo come se a noi non potesse succedere niente di male. Il contenimento delle epidemie è una responsabilità sia dei governi che della società, e noi siamo la società.

Questo articolo e il lavoro presentato sono il prodotto di una collaborazione interdisciplinare tra me (Ettore Mariotti), Nicola Lissandrini, Marco Ceccato, Matteo Zanovello e Tommaso Ceccato.

Questo Articolo è la traduzione di: https://www.linkedin.com/pulse/modelling-covid-19-outbreak-italy-ettore-mariotti

(*) Aggiornamento: Il 7 Marzo il Governo Italiano ha adottato alcuni provvedimenti importanti in questa direzione.

Si ringrazia Giampaolo Ferradini per l’aiuto alla traduzione.